
Papiga Alex vjerojatno se dosađuje.
U svojih 27 godina, 26 godina znanstvenici su ga ispitivali jednostavna pitanja poput: „Alex, koje je boje 4?”
Obično je pokazivao veliku vještinu tijekom testiranja, pregledao bi ladicu s različitim kockama, pronašao bi četiri narančaste kocke i odgovorio: „Narančaste.”
Zapravo, u testovima brojanja do četiri, točno je odgovorio na otprilike 80% pitanja. No, nakon nekog vremena postalo mu je dosadno.
Nakon dva tjedna testiranja i zurenja u ladice i kockice, ponavljanje istih riječi iznova i iznova, spremanje u kavez, sve mu je dosadilo.
Možete zamisliti iznenađenje psihologa kada je na postavljeno pitanje Alex odgovorio s: „Ništa” (eng. none). Nakon testiranja nekoliko hipoteza koje su izveli nakon Alexovog spontanog „ništa”, znanstvenici su potvrdili da je njihova sumnja bila opravdana. Alex je koristio „ništa” kako bi izrazio nulu, u ovom slučaju neprisutnost količine. Postigao je bolje rezultate kod testiranja nule (83,3%) nego kod identifikacije broja četiri.
Činjenica da je nakon što su ga znanstvenici pitali koliko je kocaka u ladici, dok u ladici zaista nije bilo niti jedne kocke, Alex točno odgovorio da ima „ništa” kocaka, znanstvenicima je zapanjujuća. Naime, prije samo nekoliko stoljeća, nula se pojavila kao simbol za „ništa” kod nas ljudi, a potom nam je trebalo neko vrijeme da je usvojimo i razumijemo kao broj.

Afričke su sive papige dugo poznate kao visoko inteligentne životinje, no shvaćanje koncepta nule je potpuno novo. (Image credits: ©iStockphoto/Thinkstock)
No opet, pod određenim okolnostima nula uopće nije broj. U nekim slučajevima nula je suprotnost beskonačnosti. U drugim slučajevima, npr. u matematičkom svijetu, ekvivalent je zapisniku i predstavlja tzv. pilot – broj za sve ostale brojeve. U svakom slučaju, izaziva maštu više nego ijedan drugi broj. Nula je također broj (uz 666, naravno) koji ima neke mračne konotacije. Kulture iz različitih vremena i na različitim prostorima dugo su izbjegavale koncept nule jer se je povezivao s iskonskom prazninom i kaosom, sastavnicima kršćanskog koncepta pakla.
Ovdje ćemo istražiti nulu kao koncept, broj i ključ matematike.
Otkriće nule
Bolje je reći da je nula otkrivena, a ne izumljena. Tu ideju podupiru mnogi.
Jedna od prvih civilizacija, grad-država Sumer u Mezopotamiji, vjerojatno je i jedna od prvih koje su se poigravale s konceptom nula kao simbolom ničega prije otprilike 5 000 godina. Na glinenim pločicama koje su se koristile za čuvanje podataka poput poreznih kartica ili izvješća o inventaru žitnice itd., par je paralelnih linija onačavao mjesto bez broja. Taj koncept nule kao mjesta na kojima se označava ništa danas uzimamo zdravo za gotovo, no u to vrijeme otkriće nule bilo je revolucionarno otkriće koje je omogućilo prikaz mnogo većih brojeva s puno manje oznaka, što je ujedno omogućilo i brže i lakše računanje.

Drevni su Sumerani prvi predstavili koncept nule. (Image credits: Photos.com/Thinkstock)
Nula kao mjesto koje označava ništa ima smisla kad proučimo niz brojeva koje koristimo danas, kao dijelove logičnog redoslijeda. Npr. broj 3024 možemo izraziti kao tri tisućice, nula stotica, dvije desetice i četiri jedinice. Bez nule na mjestu stotice, kako bismo mogli izraziti temeljnu razliku između 3024 glava stoke i 324 glave stoke?
Tisućama godina nakon Sumerana i paralela kao oznake za ništa, nula se standardizirala u Babilonu oko 300. g. pr. Kr. izumom abaka, koji nam je dao i koncept brojčanih mjesta koji koristimo i danas.
Povezanost nule i ničega nekim civilizacijama je neugodna. Tradicionalno, ništa se povezuje s kaosom i prazninom. U drugim tradicijama nula predstavlja stanje od početka svemira do nastanka čovjeka. Zbog toga su mnoge stare kulture (uključujući i Rimljane, koji su nam dali rimske brojeve) odbacile koncept nule, bilo kao oznaku za ništa ili kao broj.
Naš koncept nule kao broja, kao i arapske brojke kojim se danas koristimo, dolazi iz Indije.
Nula na zapadu i na kalendarima

Ovdje možemo vidjeti da 1. travnja pada na petak, no zato jer ne postoji 0. travnja na četvrtak, cijelokupni Gregorijanski kalendar je zapravo pogrešan. (Image credits: Creatas Images/Thinkstock)
Zapadna ideja nule kao nečeg više osim oznake za ništa došla je iz Indije u 5. st. Tada je nula započela svoj put kao broj i polako se širila arapskim svijetom. Leonardo od Pise, poznatiji kao Fibonacci, predstavio je nulu Zapadu. Budući da je bio in carinika stacioniranog u Alžiru, ne čudi što su njegovi tutori bili Arapi koji su ga i naučili matematici baziranoj na arapskim brojkama koji danas koristimo zajedno s nulom. Fibonacci je iskoristio to što je naučio te je na latinskom napisao knjigu u kojoj koristi hindu – arapske brojke i nulu 1202. godine.
Zanimljivo, nula se simultano i neovisno od Indije razvila i kod Maja u Središnjoj Americi. Za Maje je nula bila baza za početak točnog brojanja, te se to vidjelo i u majanskom kalendaru. Prvi dan mjeseca bio je nula, drugi dan bio je jedan.
Ovaj koncept puno je točniji što se tiče brojanja, a pogotovo što se tiče kalendara, te su majanski kalendari tehnički superiorniji današnjim kalendarima. Gregorijanski kalendar koji je dominantan na Zapadu temelji se rimskom načinu brojanja, koji ne uzima nulu u obzir niti u jednom obliku (iako je nastao otprilike 400 godina nakon Fibonaccijeve knjige). Prema tome, u gregorijanskom kalendaru nema godine 0 (niti 0 prije Krista, niti 0 poslije Krista). Preskačući nulu pri tim, nastaje mala ali značajna „vremenska bomba”. Zato što nema nule, nova desetljeća, stoljeća i tisućljeća započinju zapravo s godinom kasnije nego što započnu u kalendaru. Npr. ovo tisućljeće nije počelo sve do 1. siječnja 2001., iako smo ju slavili 1. siječnja 2ooo.
Ovaj nesporazum izvire iz činjenice da, ako nema nulte godine, desetljeće ne završava završetkom devete godine, kao što bi trebalo. Umjesto toga, brojenje počinje s 1, što znači da desetljeće završi prije prelaska u novo desetljeće (odnosno, stoljeće, odnosno tisućljeće).
Početak brojenja od nule je logično iako je čudno Zapadnjacima. Ako imate poteškoća s ovim, zapamtite samo da ima 10 jednoznamenkastih brojeva, od 0 do 10, sve su nadalje višeznamenkasti brojevi. No, što je s brojevima ispod nule? I tek sad počinjemo razumijevati pravo mjesto nule u matematici.
Nula u matematici
Kako bi izbjegli nepravilnost nedostatka nule u kalendaru, zapadnjački su astronomi (koji često koriste datiranje u svom radu) razvili sustav u 17. i 18. st. prema kojem se prva godina Gregorijanskog kalendara vodi kao nulta godina. Otada brojenje godina počinje s 0 (godina rođenja Isusa Krista), te godine poslije Krista rastu u plus, a godine prije Krista idu u minus. Tek je sada nula dobila mjesto koje joj pripada u beskonačnoj galaksiji brojeva.
Kao broj, nula ima specifično mjesto, točno između jedan i minus jedan. I s jedne se i s druge strane nule brojevi nižu u beskonačnost. Prema tome je nula jedini broj koji nije ni pozitivan ni negativan. Smatra se da je cijeli broj, niti pozitivan niti negativan, a opet nije uključen ni u pozitivne ni u negativne brojeve.

Nula je cijeli broj, te dok nije ni negativna ni pozitivna, istovremeno je i pozitivna i negativna. (Image credit: ©iStockphoto/Thinkstock)
Zanimljivo, iako je nula cijeli broj, ona omogućava da se brojevi razbiju na dijelove koji se izražavaju kao decimalni brojevi. Također, decimalni broj se može od nule protezati u beskonačno, te s beskonačno mnogo varijacija.
Decimalni sustav koji je nula omogućila daje nam veliku preciznost koju zahtijeva matematika i znanost. Naprimjer, bez nule bi pi, koji opisuje obujam krugova, bio nemoguć. Ovo samo podupire pretpostavku da nulu nije „izumio” čovjek, već da ju je otkrio.
Neobična svojstva nule
Činjenica da je nula istovremeno i pozitivan i negativan cijeli broj, dok nije niti pozitivan niti negativan broj, jedno je od jedinstvenih svojstava nule. Zapravo, postoji cijeli popis takvih čudnih jedinstvenosti pod nazivom svojstva nule.
Svojstvo zbrajanja s nulom proizlazi iz toga da ako se nula doda ili oduzme bilo kojem cijelom broju, rezultat je uvijek jednak tom drugom broju. Naprimjer, 5 + 0 = 5 ili 9 000 017 – 0 = 9 000 017. Kao što smo već napomenuli, nula je prikaz ničega – prema tome kad dodamo ništa nečemu, prvotno stanje se ne mijenja – nula je jedini broj koji ne mijenja niti jedan drugi broj kroz zbrajanje ili oduzimanje.
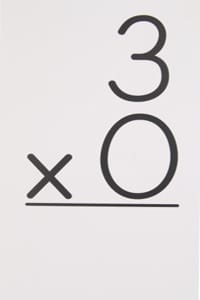
Pravilo množenja s nulom: Ako pomnožimo bilo koji broj s nulom, rezultat će biti taj broj. (Image credits: Getty Images/Thinkstock)
Inverzno zbrajanje kad je nula u pitanju, čine nulu središtem između negativnih i pozitivnih brojeva. Bilo koja dva broja čiji je zbroj nula su inverzivni brojevi jedan drugom. Naprimjer, ako -5 dodate 5, dobit ćete 0. Prema tome -5 i 5 su inverzivni brojevi jedan drugom.
Što se tiče množenja, to svaki trećoškolac zna: ako pomnožimo bilo koji broj s nulom, rezultat je uvijek nula. Jednom kad se svlada to pravilo, logika je očita, no možda nije u potpunosti jasan razlog tom pravilu. Množenje je, na neki način, prečac za zbrajanje. 3*2 je isto što i 2+2+2, te je prema tome ideja da se broj može dodati nula puta, ili da se nula može sama sebi dodavati, matematički nerazumna.
Koncept dijeljenja s nulom je i još više nerazuman, te prema tome nula tog svojstva nema; koncept dijeljenja s nulom jednostavno ne postoji jer se ne može izvesti. Čak se i matematičari muče kako bi objasnili zašto ne funkcionira dijeljenje s nulom. Razlog tome je usko vezan za svojstvo množenja s nulom. Kada dijelimo neki broj s drugim brojem, na primjer 6/2, rezultat (u ovom slučaju 3) će se uklopiti u obratnu formulu, gdje rezultat pomnožen s djeliteljom daje djeljenika. Drugim riječima: 6/2 = 3 i 3*2 = 6. To pravilo ne funkcionira s nulom; 3*0 = 0 i 0*0 = 0 (ne dobijemo djeljenika).
Izvor: HowStuffWorks



