Zašto postoji toliko veza između Fibonaccijevog niza i prirode? Postoji li magična jednadžba koja bi otkrila tajne svemira? Vjerojatno ne, ali zahvaljujući čovjeku u srednjem vijeku, koji je bio opsjednut zečevima, imamo niz brojeva koji opisuje mnoge uzorke u prirodi.
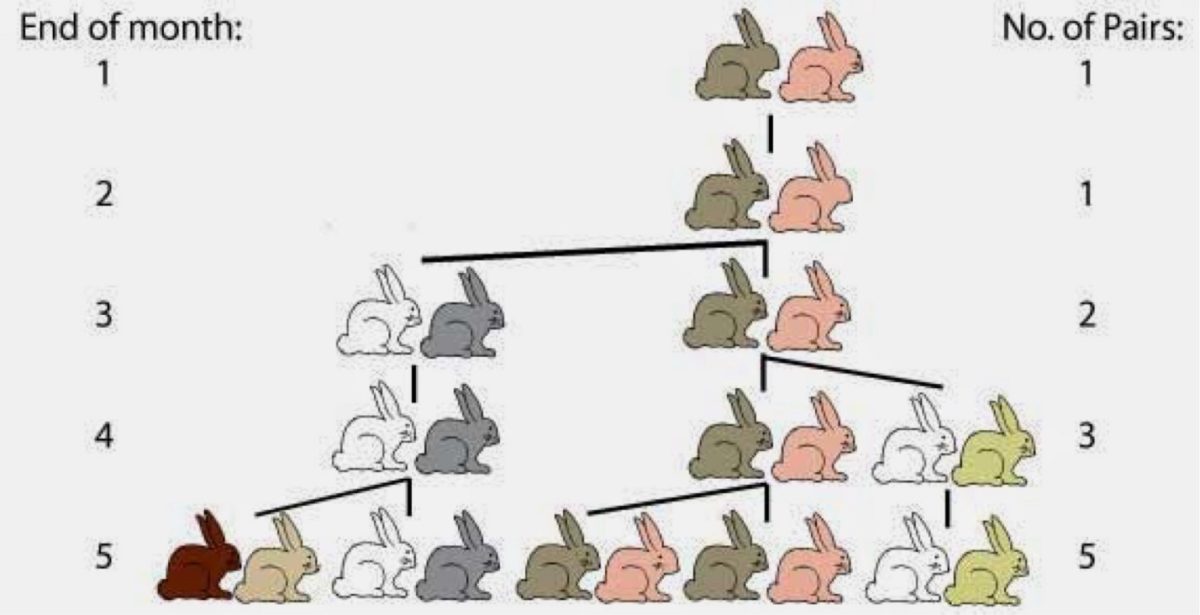
1202. godine, talijanski matematičar Leonardo Pisano, poznatiji kao Fibonacci, postavio je pitanje: „U idealnim uvjetima, koliko parova zečeva možemo dobiti u godini dana od jednog para zečeva?“
Ovaj eksperiment se bazira na uvjetu da ženka uvijek rađa parove i da se svaki par sastoji od mužjaka i ženke. Dva novorođena zeca stavljaju se u ograđeno mjesto gdje se dalje razmnožavaju. Zečevi se ne mogu razmnožavati dok nisu bar godinu dana stari pa prvi mjesec postoji samo jedan par zečeva. Na kraju drugog mjeseca ženka leže što nam daje dva para zečeva. Treći mjesec prvi par zečeva ima još jedan par novorođenčadi. Tako imamo tri para zečeva od kojih će dva para imati mlade idući mjesec.
Niz kojim se zečevi razmnožavaju glasi: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144 i tako u beskonačnost. Svaki idući broj u nizu je zbroj dva prethodna. Ovaj niz poznat je kao Fibonaccijev niz. Omjer između brojeva niza približava se tzv. Zlatnom rezu (1.618034).
Na prvi pogled Fibonaccijev eksperiment nudi jako malo u stvarnom svijetu ali on se često može naći u prirodi. Ako želite vidjeti kako se ti brojevi manifestiraju u prirodi ne morate promatrati zečeve. Jedino što trebate je pogledati oko sebe.
Fibonaccijev niz i zlatni rez
Fibonaccijev niz nećete naći svugdje u prirodi. Mnoge biljke i životinje imaju drugačije nizove brojeva. Samo zato što niz brojeva može biti primijenjen na nekom fizičkom objektu ne znači da postoji veza. Nekada je slučajnost jednostavno slučajnost ali Fibonaccijev niz se u prirodi pojavljuje toliko često da možemo vidjeti vezu između uzoraka. Tu vezu često možete primijetiti ako promatrate na koji način različite biljke rastu.
Evo nekoliko primjera:
Suncokret: Pogledajte red sjemena u centru suncokreta i primijetit ćete nešto što izgleda kao spiralni uzorak. Ako prebrojite te spirale dobiti ćete Fibonaccijev broj. Ako podijelite spirale koje idu prema lijevo s onima koje idu desno dobiti ćete dva Fibonaccijeva broja.
Cvijeće: Ako prebrojite latice na nekom cvijetu, suma će vrlo često biti jedan od brojeva Fibonaccijevog niza.
Pčele: Svaka kolonija pčela sastoji se od kraljice, par trutova i puno radnika. Ženke pčela (kraljice i radnici) imaju dva roditelja, truta i kraljicu. Trutovi se pak roje iz neoplođenih jajašca. To znači da imaju jednog roditelja. Fibonaccijev niz označuje trutovo obiteljsko stablo u kojem on ima jednog pretka, zatim dva pretka, tri pretka i tako dalje.
Ljudsko tijelo: Pogledajte se u ogledalo i vidjet ćete Fibonaccijev niz. Vaše tijelo se sastoji od brojeva 1, 2, 3 i 5. Imate jedan nos, dva oka, tri segmenta svakog ud-a i pet prstiju na svakoj ruci. Izmjerimo li čovječju dužinu od vrha glave do poda, zatim do podijelimo s dužinom od pupka do poda dobijemo 1.618034, a to je broj kojem se Fibonaccijev niz približava.
Zašto postoji toliko veza između Fibonaccijevog niza i prirode? Znanstvenici su godinama pokušali odgovoriti na to pitanje. U nekim slučajevima to bi mogla biti slučajnost, u drugim slučajevima to je tako jer određeni uzorak rasta je najefikasniji kada prati zlatni rez. Kod biljaka to znači optimalan omjer svjetla na svakoj latici ili optimalan položaj sjemenki.
Mnogo je primjera gdje se Fibonaccijev niz može upotrijebiti, a neki od vas vjerojatno su čuli i za Fibonaccijevu strategiju klađenja, popularno kod nekih profesionalnih kladioničara.



